METHODS OF COMPUTATIONAL PHYSICS (Spring 2025)

Course Number: Phys 516
Class Number: 50614R
Instructor: Aiichiro Nakano; office: VHE 610; email: anakano@usc.edu
TA: Logan Yamamoto; email: lkyamamo@usc.edu
Lecture: 9:00-9:50 M W F, KAP 145
Office Hour: 16:00-17:20 F, VHE 610
Class homepage: https://aiichironakano.github.io/phys516.html
Textbooks:
T. Pang, "An Introduction to Computational Physics, 2nd Ed." (Cambridge Univ. Press, 2010)--sample C, Fortran 77, and Fortran 90 programs available on line.
W. H. Press, B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling, "Numerical Recipes, 3rd Ed." (Cambridge Univ. Press, 2007)--available online.
R. Li and A. Nakano, Simulation with Python (APress, 2022)--codes.

Prerequisites: Basic knowledge of calculus and undergraduate physics; familiarity with a programming language such as C, Fortran, or Python -- A nice introduction to computing: (1) Y. Patt and S. Patel, Introduction to Computing Systems: From Bits and Gates to C and beyond, (2) T. Hey and G. Papay, The Computing Universe; Software skills for computational physicists: A. Scopatz and K. D. Huff, Effective Computation in Physics, USC students have free access through Safari Online.

Course Description

Students will learn basic elements of computational methods and acquire hands-on experience in their practical use in the context of computer simulations to solve physics problems. For details, please see course information sheet.

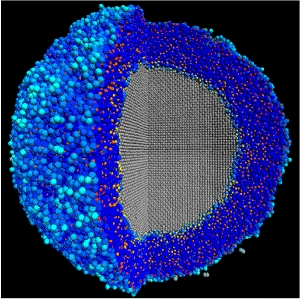
Molecular dynamics simulation of the oxidation of an aluminum nanoparticle.

Announcements

• 1/13 (M): Class begins.
• 1/17 (F): Assignment 1 discussion at office hour (3:00 pm in VHE 610); please note the special time this week.
• 1/17 (F): Physics happy hour at 4 pm in the ACB Courtyard.
• 1/20 (M): MLK Birthday--no class.
• 1/22 (W): Please use the Brightspace discussion forum to exchange information and ideads.
• 1/22 (W): Assignment 1 due at 11:59 pm.
• 1/24 (F): Exploring Together: US-Japan Space Collaboration Symposium at 1:30 pm.
• 1/27 (M): CECAM Marvel classic lecture on quantum Monte Carlo by Prof. David Ceperley (Univ. of Illinois) at 6 am.
• 1/27 (M): Seminar on quantum many-body physics in the noisy era by Dr. Abhinav Prem (Institute for Advanced Studies) at 4:15 pm (SSL 202).
• 1/29 (W): See note on DeepSeek.
• 1/30 (Th): More on DeepSeek.
• 1/31 (F): Assignment 2 due at 11:59 pm; what to submit: 2 source codes (mean-stdv.c & stdv.c), 2 plots, 1 proof.
• 2/3 (M): Seminar on nonlinear spectral model reduction from data by Prof. George Haller (ETZ Zurich) at 4:00 pm (RTH 526).
• 2/3 (M): Seminar on condensed matter theory in the quantum information era by Dr. Pablo Sala (Caltech) at 4:15 pm (SSL 202).
• 2/4 (T): Oscar goes to Prof. Jernez Barbic in computer science for his physically accurate solvers.
• 2/7 (F): Assignment 3 discussion at office hour (3:00 pm in VHE 610); please note the special time this week.
• 2/7 (F): Physics happy hour at 4 pm in the ACB Courtyard.
• 2/10 (M): Seminar on talking the measure of quantum dynamics by Dr. Yaodong Li (Stanford) at 4:15 pm (SSL 202).
• 2/10 (M): Assignment 3 due at 11:59 pm; what to submit: 1 proof, 1 source code, 2 plots.
• 2/12 (W): registration is open for 3rd Drug Discovery Innovation Workshop on Feb. 28 (F).
• 2/17 (M): President's Day--no class.
• 2/24 (M): Seminar on non-invertible symmetry in the quantum world by Dr. Ho Tat Lam (MIT) at 4:15 pm (SSL 202).
• 2/26 (W): Seminar on "theoretical foundations of neuroAI" by Prof. Paul Bogdan (USC) at 10 am (OHE132).
• 2/26 (W): See the news on Microsoft's new Majorana 1 quantum processor.
• 2/28 (F): Assignment 4 due at 11:59 pm.
• 3/3 (M): Seminar on many-body effects on exciton dynamics and nonlinear optics in low-dimensional materials by Prof. Diana Y. Qiu (Yale) at 4:15 pm (SSL 202).
• 3/10 (M): Seminar on driving quantum matter out-of-equilibrium by Prof. Prineha Narang (UCLA) at 4:15 pm (SSL 202).
• 3/10 (M): Assignment 5 due at 11:59 pm.
• 3/13 (Th) - 14 (F): USC Symposium on the Future of Computing.
• 3/17 (M) - 21 (F): Spring Recess--no class.
• 3/31 (M): Please sign up for a 2-minute final-project presentation.
• 3/31 (M): Assignment 6 due at 11:59 pm.
• 4/4 (F): Physics happy hour at 4 pm in the ACB Courtyard; accordingly, special time for office hour at 3-4 pm.
• 4/9 (W): You are welcome to PHYS 650 (topics in current research: quantum mechanics & supercomputing) at 3 pm in ACB 536.
• 4/18 (F): You are welcome to the CS PhD student mixer at 4 pm in GCS Lower Level 1; this substitutes for the regular office hour, so we discuss in GCS instead of VHE; to attend, please RSVP by 4/15 (T).
• 4/21 (M): Seminar on "computational cellular mechanobiology" by Prof. Padmini Rangamani (UCSD) at 4:00 pm (RTH 526).
• 4/21 (M): Seminar on the physics of self-organization by Prof. Cristina Marchetti (UCSB) at 4:15 pm (SSL 202).
• 4/23 (W): See Bohm in Brazil workshop (July 15-18, Sao Paolo, Brazil); see also David Bohm.
• 4/25 (F): For quantum computing hands-on, please create an account at IBM Quantum.
• 4/25 (F): Assignment 7 due at 11:59 pm.
• 4/28 (M): You are welcome to CSCI 697 (seminar in computer science research: quantum mechanics & supercomputing) at 12 pm in SGM 101.
• 4/28 (M): See the Viterbi Magazine article on Just Dance.
• 4/30 (W): Register for CyberMAGICS Workshop on cyber-training on materials genome innovation for computational software (June 5-6, 2025).
• 5/14 (W): Final-project report due; don't forget to submit it to Brightspace.

Class Schedule

• 1/13 (M): Course information & logistics; final-project publications; Math quiz
• 1/15 (W): Introduction; Nobel prizes in 2024
• 1/17 (F): Assignment 1 discussion -- computing and math preparation; simple mathematics
• 1/22 (W): Monte Carlo (MC) basics: notes and slides
• 1/24 (F): Assignment 2, part 1 discussion -- hands-on MC
• 1/27 (M): Assignment 2, part 2 discussion -- nonuniform random number generation by coordinate transformation -- see frequently asked questions on assignment 2 and all assignments
• 1/29 (W): Metropolis MC algorithm
• 1/31 (F): MC simulation of spins: notes and slides
• 2/3 (M): Assignment 3 discussion
• 2/5 (W): Metropolis MC simulation Q&A
• 2/7 (F): Fluctuation-dissipation theorem; unitary time propagation; linear response; cf. advanced Monte Carlo algorithms
• 2/10 (M): Numerical integration and Gaussian quadratures; recurisive formula for Legendre polynomials; Numerical Recipes, Sec. 4.5; fast multipole method
• 2/12 (W): Molecular dynamics (MD) basics; slides; Michael Levitt's Nobel lecture in 2013
• 2/14 (F): MD technical details; Lennard-Jones Q&A
• 2/19 (W): Assignment 4 (MD), part 1 discussion -- Liouville's theorem
• 2/21 (F): Assignment 4 (MD), part 2 discussion -- velocity autocorrelation; nucleation theory
• 2/24 (M): Assignment 4 (MD), part 3 discussion -- split-operator formalism; MD simulation Q&A
• 2/26 (W): Quantum dynamics (QD) basics: split-operator and spectral methods; slides
• 2/28 (F): Assignment 5 (QD), part 1 discussion -- split-operator method; lecture on spectral method
• 3/3 (M): Assignment 5 (QD), part 2 discussion -- spectral-method programming
• 3/5 (W): Assignment 5 (QD), part 3 discussion -- quantum tunneling
• 3/7 (F): Spectral method and fast Fourier transform (FFT); note on unitary time-propagators; quantum Fourier transform
• 3/10 (M): Iterative energy minimization for quantum molecular dynamics; Numerical Recipes, Sec. 10.6 on the conjugate-gradient method; see PHYS 760: Extreme-scale Quantum Simulations
• 3/12 (W): Tight binding (TB) model of electronic structures; slides
• 3/14 (F): Computing TB Hamiltonian elements by projection; assignment 6 discussion; energy band
• 3/24 (M): Newton method for root finding; slides
• 3/26 (W): O(N) Fermi-operator expansions; eigensystems: note and slides
• 3/28 (F): Singular value decomposition (SVD) and density matrix (notes on SVD and polar decomposition; slides; Numerical Recipes, Sec. 2.6); Lanczos method for eigensystems (slides and supplementary notes); Cholesky decomposition (notes and Numerical Recipes, Sec. 2.9)
• 3/31 (M): Final project discussion; see notes on final projects and Whitesides' group: writing a paper, G. M. Whitesides, Adv. Mater. 16, 1375 (2004)
• 4/2 (W): Final project ideas exchange; please attend the class phsyically
• 4/4 (F): Monte Carlo simulation of stochastic processes; slides
• 4/7 (M): Assignment 7, part I (stochastic simulation) discussion
• 4/9 (W): Option price; Viterbi algorithm
• 4/11 (F): Quantum Monte Carlo simulation; slides; path-integral molecular dynamics (PIMD)
• 4/14 (M): Assignment 7, part II (QMC) discussion
• 4/16 (W): Kinetic Monte Carlo (KMC) simulation; motivating slides
• 4/18 (F): KMC algorithm and electron-transfer simulation
• 4/21 (M): Assignment 7, part III (KMC) discussion
• 4/23 (W): KMC theory and transition state theory; suppl. 1: Liouville equation; suppl. 2: master equation; suppl. 3: transition state theory; suppl. 4: kinetic Monte Carlo simulation
• 4/25 (F): Quantum dynamics simulations on quantum computers: slides; qubits and quantum circuits
• 4/28 (M): Transverse-field Ising model: lecture note; Qiskit code; Phys 516 summary (where to go from here)
• 4/30 (W): Final-project presentation, part I; see all-star roster
• 5/2 (F): Final-project presentation, part II